Praca doktorska

SPIS TREŚCI

WYKAZ WAŻNIEJSZYCH OZNACZEŃ STOSOWANYCH W PRACY 5

WSTĘP 6

1. NUMERYCZNY MODEL TERENU 10

WPROWADZENIE 10

1.1 OGÓLNE ZASADY PRZEDSTAWIANIA INFORMACJI O TERENIE 11

1.2 WYBÓR RODZAJU NUMERYCZNEGO MODELU TERENU 11

1.3 RODZAJE OBIEKTÓW NA MAPACH I SPOSÓB ICH PRZEDSTAWIENIA W NMT 12

1.4 MODEL MATEMATYCZNY TERENU NA BAZIE DANYCH UZYSKANYCH Z DIGITALIZACJI MAPY TOPOGRAFICZNEJ 13

1.4.1. Modelowanie obiektów punktowych 14

1.4.2 Modelowanie obiektów powierzchniowych 14

1.4.3 Modelowanie obiektów liniowych 19

2. MODEL SIECI TRAS PRZEJAZDU 27

WPROWADZENIE 27

2.1 MODEL ZGRUBNEJ STP 27

2.2 MODEL DOKŁADNEJ STP 33

2.2.1 Zasada opisu i tworzenia drzewa czwórkowego 34

2.2.2 Obliczanie wysokości zp punktu o danych współrzędnych płaskich xp,yp 37

2.2.3 Algorytmy tworzenia podziału terenu i określenia dokładnej STP 42

3. ALGORYTMY PLANOWANIA PRZEMIESZCZANIA RÓWNOLEGŁEGO KOLUMN W SIECI O STRUKTURZE STAŁEJ 55

WPROWADZENIE 55

3.1 ZDEFINIOWANIE PROBLEMU WYZNACZANIA PLANU PRZEGRUPOWANIA 55

3.2 ALGORYTM PEŁNEGO PRZEGLĄDU WYZNACZANIA NAJKRÓTSZEJ RÓWNOLEGŁEJ K-DROGI 60

3.3 ALGORYTM PODSTAWOWY WYZNACZANIA NAJKRÓTSZEJ RÓWNOLEGŁEJ K-DROGI (NRKD) 69

3.3.1 Opis algorytmu NRKD 71

3.3.2 Oszacowanie złożoności algorytmu NRKD 84

3.3.3 Porównanie algorytmu NRKD z innymi metodami 90

3.3.4 Metoda oceny optymalności rozwiązania z algorytmu NRKD 94

3.4 ROZSZERZENIA ALGORYTMU NRKD 100

3.4.1 Wprowadzenie wielu wierzchołków początkowych i końcowych dla każdej z kolumn obiektów 100

3.4.2 Wprowadzenie ograniczenia na czas przegrupowania 101

3.4.3 Wprowadzenie ograniczenia na "bezpieczność" wyznaczanych tras 102

3.4.4 Wprowadzenie ograniczenia na wyrównanie czół kolumn 108

3.5 METODA WYZNACZANIA RÓWNOLEGŁEJ K-DROGI e-NAJKRÓTSZEJ 111

4. ALGORYTMY PLANOWANIA PRZEMIESZCZANIA RÓWNOLEGŁEGO KOLUMN
W SIECI O STRUKTURZE ZMIENNEJ 117

WPROWADZENIE 117

4.1 METODA WYZNACZANIA K-DROGI NAJLEPSZEJ W SIECI ZAWODNEJ BEZ ZALEŻNOŚCI PRAWDOPODOBIEŃSTW I OD DŁUGOŚCI ODCINKA CZASU PRZEBYWANIA NA K-DRODZE 118

4.2 METODY WYZNACZANIA K-DROGI NAJLEPSZEJ W SIECI ZAWODNEJ Z ZALEŻNOŚCIĄ PRAWDOPODOBIEŃSTW I OD DŁUGOŚCI ODCINKA CZASU PRZEBYWANIA NA K-DRODZE 127

4.2.1 Algorytmy wyznaczania K-drogi niezdominowanej 129

4.2.2 Algorytm wyznaczania K-drogi pseudo-kompromisowej 131

4.3 MODEL NISZCZENIA SIECI TRAS PRZEJAZDU 134

4.4 METODA SYMULACYJNA WYZNACZANIA K-DROGI NAJLEPSZEJ 143

5. PORÓWNANIE WYNIKÓW BADAŃ ALGORTYMÓW PLANOWANIA
PRZEMIESZCZANIA RÓWNOLEGŁEGO KOLUMN W SIECIACH
O STRUKTURZE ZMIENNEJ 148

WPROWADZENIE 148

5.1 WYNIKI BADAŃ SYMULACYJNYCH DLA SIECI SZGR 151

5.2 WYNIKI BADAŃ SYMULACYJNYCH DLA SIECI SDOK 158

5.3 PORÓWNANIE WYNIKÓW DLA RÓŻNYCH DŁUGOŚCI CZASOWYCH KOLUMN 164

5.4 PORÓWNANIE WYNIKÓW DLA RÓŻNYCH ODSTĘPÓW CZASU MIĘDZY INFORMACJAMI O STANIE STRUKTURY SIECI 165

5.5 PORÓWNANIE WYNIKÓW DLA RÓŻNEJ LICZBY KOLUMN 166

UWAGI I WNIOSKI 168

DODATEK. CHARAKTERYSTYKA KOMPUTEROWEGO SYSTEMU WSPOMAGANIA
I OCENY PLANOWANIA PRZEGRUPOWANIA KOLUMN 174

LITERATURA 179

STRESZCZENIE

W pracy rozważa się zadanie badawcze, polegające na opracowaniu planu równoległego przemieszczania obiektów w sieci dróg. Struktura sieci może być niezmienna w czasie, bądź może ulegać dynamicznym zmianom. Z kolei przemieszczane obiekty mogą nie być obiektami punktowymi, czyli mogą posiadać tzw. długość czasową. Zadanie badawcze sprowadzono do problemu wyznaczania planu przegrupowania kilku kolumn obiektów wojskowych w sieci bazującej na rzeczywistym terenie działań, w warunkach bez oddziaływa nia (struktura stała) i z oddziaływaniem (struktura zmienna) na strukturę sieci (np. niszczeniem przez przeciwnika), co nie zmniejsza możliwości szerokiego zastosowania zaprezentowanego rozwiązania.

Problem wyznaczania planu przegrupowania dla wielu kolumn obiektów jest problemem nie tylko analitycznym. W symulacji działań bojowych jest to jeden z podproblemów, które należy rozwiązać, aby zamodelować przemieszczanie się obiektów, np. po mapie komputerowej. Istotnym elementem jest posiadanie cyfrowego zapisu terenu działań. Posiadanie takiej informacji umożliwia chociażby określenie przejezdności interesujących nas fragmentów terenu.

Wyznaczanie planu przegrupowania dla wielu kolumn jest problemem bardzo złożonym i w związku z tym, w wielu pracach problem ten rozpatrywany jest na różnych poziomach szczegółowości ([5], [8], [16], [69], [94], [98], [99], [106], [121], [130], [131]). Zagadnienie to znacznie się komplikuje, z tego względu, że kolumny marszowe są rozciągnięte na pewnej długości, a w związku z tym określone wierzchołki i drogi w pewnych okresach czasu są zajęte przez daną kolumnę. Wobec powyższego w pewnych odcinkach czasu nie będzie możliwości przejazdu przez dany wierzchołek czy odcinek (łuk) drogi. Zajętość ta może wynikać również z działalności jednostek nadrzędnych. Ponadto, w rzeczywistych warunkach przegrupowania, sieć po której przegrupowują się kolumny może ulegać niszczeniu przez potencjalnego przeciwnika.

Algorytmy przegrupowania bazują z reguły na znanych algorytmach znajdowania najkrótszych dróg w sieciach. W literaturze dotyczącej tego tematu można znaleźć rozwiązania wielu problemów dotyczących najkrótszych dróg począwszy od algorytmów podstawowych: Dijkstry [33] i Floyda [42], poprzez różne modyfikacje algorytmów podstawowych ([3], [4], [10], [27], [35], [59], [67], [95], [101], [120]), algorytmy znajdowania N-tej najkrótszej drogi ([53], [57], [60], [62], [86], [87], [110], [116]), aż po algorytmy znajdowania najkrótszych dróg w sieciach uwarunkowanych czasowo ([13], [22], [135]). Można również spotkać szereg algorytmów poświęconych wyznaczaniu dróg najkrótszych w sieciach, których gałęzie opisane są wektorem wag ([26], [91], [101], [137], [140]) lub badana sieć jest stochastyczna (w sensie wag lub struktury) [23], [44], [74], [75], [76], [85], [91], [111], [134]. Większość z tych algorytmów można, z mniejszym lub większym trudem, zaadoptować do problemu wyznaczanie planu przegrupowania dla wielu kolumn obiektów.

Podsumowując, celem niniejszej pracy jest zdefiniowanie problemu równoczesnego przegrupowania kolumn obiektów (np. wojskowych) w sieci tras przejazdu bazującej na rzeczywistym terenie, w warunkach bez oddziaływania i z oddziaływaniem na strukturę sieci przez potencjalnego przeciwnika oraz opracowanie algorytmów, wraz ze sposobem ich oceny, umożliwiających wyznaczenie rozwiązania problemu, które wspomagałyby podejmującego decyzję przy planowaniu przegrupowania. Dodatkowym wynikiem pracy mogłoby być pokazanie możliwości szerszego zastosowania prezentowanych rozwiązań.

W pracy przedstawiono model równoległego przegrupowania wielu kolumn obiektów w sieci. Opracowano numeryczny model terenu (NMT) oraz wykorzystano NMT do wyznaczenia dwupoziomowego modelu sieci tras przejazdu (STP) wykorzystywanej w zadaniu wyznaczania optymalnego planu przegrupowania kolumn. Zdefiniowano pojęcie K-drogi oraz pokazano, że problem wyznaczania optymalnego planu przegrupowania może być sprowadzony do problemu wyznaczania najkrótszej K-drogi w sieci. Opracowano algorytmy wyznaczania najlepszej K-drogi w sieciach o strukturze stałej i zmiennej oraz oszacowano ich złożoność obliczeniową. Zaproponowano model niszczenia sieci tras przejazdu oraz opracowano symulacyjną metodę badania jakości opracowanych algorytmów do wyznaczania K-drogi najlepszej w niszczonej sieci. Zamieszczono wyniki działania programu pozwalającego na ocenę opracowanych algorytmów oraz podano metodę wspomagania wyznaczania planu przegrupowania w oparciu o uzyskane wyniki symulacji dla wybranych planów niszczenia sieci.

W rozdziale pierwszym zaprezentowano numeryczny model terenu na bazie danych z digitalizacji mapy topograficznej, zorientowany zwłaszcza na te elementy terenu, które są istotne z punktu widzenia jego przekraczalności dla różnych obiektów wojskowych.

W rozdziale drugim przedstawiono dwupoziomowy, w sensie szczegółowości, model sieci tras przejazdu, które są bazą dla algorytmów wyznaczania optymalnego planu przegrupowania. Model pierwszy sieci (sieć zgrubna) oparto o istniejące w rzeczywistym terenie drogi. Opracowane w tym rozdziale algorytmy podziału terenu, bazujące na stworzonym wcześniej NMT, na kwadraty obszarów jednorodnych topograficznie, posłużyły do utworzenia dokładnej sieci tras przejazdu (model drugi sieci).

Rozdział trzeci zawiera sformułowanie zadania wyznaczania optymalnego planu przegrupowania kolumn obiektów oraz definicję pojęcia K-drogi najkrótszej. W celu pokazania złożoności problemu zaprezentowano algorytm pełnego przeglądu do wyznaczania równoległej K-drogi najkrótszej. Następnie przedstawiono algorytm podstawowy wyznaczania najkrótszej równoległej K-drogi (NRKD) wraz z oszacowaniem jego złożoności obliczeniowej. Pokazano, że algorytm ten może nie być optymalny i zaproponowano metodę symulacyjną oszacowania prawdopodobieństwa otrzymania rozwiązania optymalnego z algorytmu NRKD w pewnej klasie sieci. Porównano algorytm NRKD z innymi spotykanymi w literaturze algorytmami, które można potencjalnie zaadoptować do badanego problemu. Rozszerzono i rozwiązano problem wyznaczania NRKD o przypadki:

- kiedy dla każdej z kolumn obiektów dysponujemy więcej niż jednym wierzchołkiem początkowym i (lub) końcowym,
- kiedy dysponujemy górnym ograniczeniem na moment dotarcia kolumn do miejsc docelowych,
- kiedy dysponujemy ograniczeniami (dolnymi i (lub) górnymi) na odległości między drogami dla sąsiednich kolumn oraz, kiedy żądamy aby czoła przegrupowujących się kolumn znajdowały się w ustalonych wierzchołkach sieci w tym samym czasie.

Zdefiniowano i podano metodę rozwiązania problemu znajdowania K-drogi e -najkrótszej charakteryzującej się tym, że jest (1+e ) razy gorsza (w sensie długości) od potencjalnie najlepszej.

W rozdziale czwartym przedstawiono algorytmy wyznaczania najlepszej K-drogi w sieci zawodnej. Rozważono przy tym dwa rodzaje zawodności :

- kiedy rozkład prawdopodobieństwa czasu do zniszczenia elementu sieci (wierzchołka lub łuku) nie zależy od czasu dotarcia do tego elementu sieci;
- kiedy rozkład prawdopodobieństwa czasu do zniszczenia elementu sieci (wierzchołka lub łuku) zależy od czasu dotarcia do tego elementu sieci;

Zaproponowano model niszczenia sieci oraz metodę analityczną wyznaczenia rozkładów prawdopodobieństwa czasów życia elementów STP w proponowanym modelu niszczenia. Podano metodę symulacyjną oceny algorytmów wyznaczania najlepszej K-drogi w sieci zawodnej. W metodzie tej uwzględniono, m.in. częstość docierania informacji o stanie struktury sieci do poruszających się kolumn.

W rozdziale piątym zaprezentowano wyniki symulacyjnych badań algorytmów dla wybranych planów niszczenia sieci. Na podstawie badań symulacyjnych :

- zaproponowano sposób podejmowania decyzji o wyborze algorytmu do wyznaczania K-drogi najkrótszej przy badanych planach niszczenia sieci,
- pokazano jaki wpływ na rozwiązanie ma częstośc informacji o stanie struktury sieci, -
- pokazano jaki wpływ na rozwiązanie ma długość czasowa kolumn oraz ich liczba,
- zaproponowano sposób ustalenia optymalnego przedziału czasu otrzymywania informacji o stanie struktury sieci.

W Uwagach i Wnioskach podsumowano wyniki badań nad rozpatrywanym zadaniem badawczym oraz zaproponowano kierunki dalszych prac dotyczące tego zagadnienia.

W Dodatku przedstawiono opis aplikacji, która powstała w trakcie realizacji zadania badawczego. Spełnia ona dwie funkcje:

- środowiska do przeprowadzenia badań, których wyniki zaprezentowano w niniejszej pracy;
- narzędzia komputerowego wspomagania planowania równoległego przemieszczania kolumn w warunkach bez oddziaływania i z oddziaływaniem na strukturę sieci potencjalnego przeciwnika.

Przedstawione w pracy rozwiązanie problemów wtórnych skupiających się wokół problemu pierwotnego - planowania równoległego przegrupowania kolumn - znalazło zastosowanie w pracach prowadzonych w Wydziale Cybernetyki w ramach projektów naukowo-badawczych dotyczących komputerowej symulacji działań bojowych ([126], [127], [128]). Aplikacja opisana w Dodatku, jako moduł planowania przegrupowania, stanowi część komputerowego systemu wspomagania i oceny decyzji w działaniach bojowych, który powstał w ramach tych prac.

DODATEK

Charakterystyka komputerowego systemu wspomagania i oceny planowania przegrupowania kolumn

W celu przeprowadzenia badań, których wyniki zaprezentowano w pracy, oprogramowano wybrane elementy dotyczące rozpatrywanego zadania badawczego. Oprogramowanie to wykonano przy użyciu zorientowanego obiektowo języka symulacyjnego - MODSIM II, wykorzystywanego od kilku lat w Wydziale Cybernetyki WAT. W celu graficznego zobrazowania danych i wyników wykorzystano dodatkowo pakiety SIMGRAPHICS i SIMOBJECT ułatwiające projektowanie grafiki oraz okien dialogowych w środowisku języka MODSIM.

Wygląd okna głównego aplikacji przedstawiono na rys. D.1.

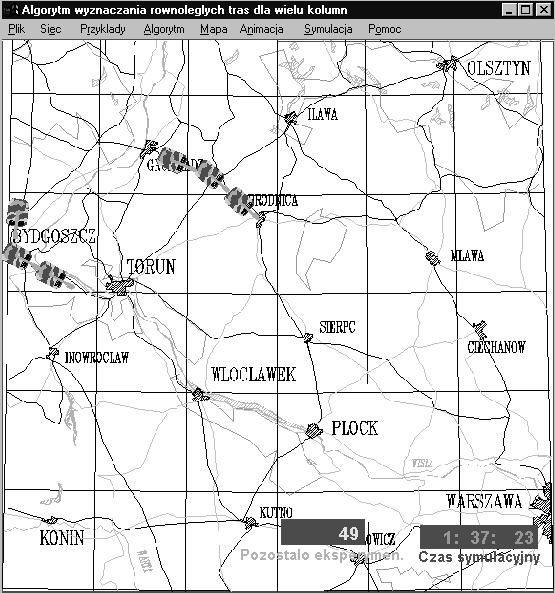
Rys. D.1 Wygląd okna głównego aplikacji w trakcie realizacji eksperymentu symulacyjnego

Prezentowane oprogramowanie składa się z czterech zasadniczych modułów:

- wejścia-wyjścia (opcja "Plik" z rys. D.1);
- edycji sieci (opcja "Sieć" z rys. D.1);
- analizy algorytmów dla sieci o stałej i zmiennej strukturze (opcja "Algorytm" z rys. D.1);
- symulacyjnego badania algorytmów w sieci o zmiennej strukturze (opcja "Symulacja" z rys. D.1);

Moduł pierwszy zawiera możliwości zapisania i odczytania modelu sieci (tzn. jej struktury, macierzy wag, charakterystyk probabilistycznych opisanych na elementach struktury sieci, podkładu mapowego, itp.).

Moduł drugi składa się z kilku części. Pierwsza z nich umożliwia zbudowanie sieci w sposób "ręczny" poprzez dodawanie (bądź usuwanie) wierzchołków sieci w oknie programu (np. w oparciu o podkład mapowy wcześniej wczytany - opcja "Mapa" z rys. D.1) oraz połączenie wybranych wierzchołków łukami i określenie charakterystyk tych łuków (waga, rozkład prawdopodobieństwa czasu do zniszczenia łuku). Każdy wierzchołek opisany jest współrzędnymi względem lewego dolnego rogu okna programu (mapy).

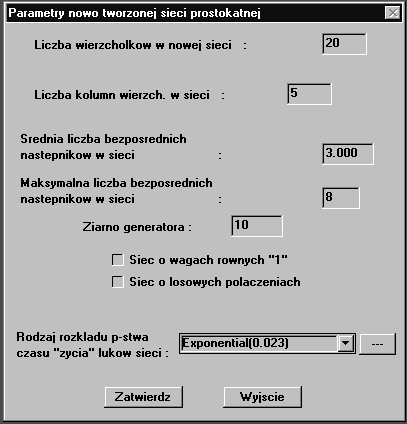
Rys. D.2 Okno dialogowe generatora sieci prostokątnej

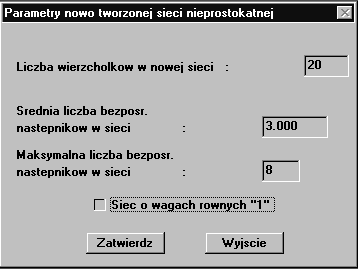
Rys. D.3 Okno dialogowe generatora sieci nieprostokątnej

Drugą część modułu stanowią generatory sieci o podanych własnościach. Aby wygenerować sieć prostokątną (pełną lub niepełną) należy podać następujące parametry (rys. D.2) :

- liczbę W wierzchołków sieci;
- średnią n_gavg liczby bezpośrednich następników w sieci;
- maksymalną n_max liczbę bezpośrednich następników w sieci;
- rozkład (oraz parametry) prawdopodobieństwa czasu do zniszczenia elementów sieci, wybierany spośród następujących typów rozkładów: wykładniczego, normalnego, równomiernego, trójkątnego, Weibulla, Erlanga, funkcji niezawodności rozkładu wykładniczego, stablicowanego, jednopunktowego. Rozkład jednopunktowy z parametrem t=0 może zostać użyty do zamodelowania braku niszczenia łuków sieci, bo P(T < t=0) = 0;
- liczbę j kolumn, w których zostaną wyświetlone wierzchołki sieci;
- informację, czy dana sieć prostokątna ma być siecią pełną, czy niepełną;

Do wygenerowania sieci nieprostokątnej wystarczą pierwsze cztery parametry z wyżej wymienionych (rys. D.3).

Każda z sieci może zostać przedstawiona w postaci macierzy wag lub w postaci graficznej. Dodatkowo sieć można wyświetlić na odpowiednim podkładzie mapowym. Przesuwając wierzchołki sieci możemy w prosty sposób zgrać faktyczną informację z mapy, ze strukturą sieci.

Trzeci moduł umożliwia zbadanie poszczególnych algorytmów zaprezentowanych w pracy, zarówno w sieci o stałej, jak i zmiennej strukturze. Aby przeprowadzić badania tych algorytmów należy podać następujące parametry (rys. D.4):

- liczbę K kolumn przemieszczanych obiektów;
- K-wierzchołki: początkowy i^s i końcowy i^d;
- długość czasową każdej z kolumn;
- rodzaj algorytmu;
- górne ograniczenie na czas przegrupowania.

Wyniki działania algorytmów przedstawiane są w postaci, jak na rys. D.5. Dodatkowo, jeżeli sieć poddawaną badaniu przedstawiono w postaci graficznej, to K-droga wynikowa również zostanie przedstawiona w sieci w takiej postaci.

Moduł ten umożliwia również zbadanie prawdopodobieństwa otrzymania rozwiązania optymalnego z algorytmu NRKD. Aby przeprowadzić te badania należy podać następujące parametry (rys. D.6):

- liczbę E powtórzeń eksperymentu;
- klasę (lub klasy) sieci, dla których przeprowadzimy badania.

Rys. D.4 Okno dialogowe algorytmów wyznaczania K-drogi najkrótszej

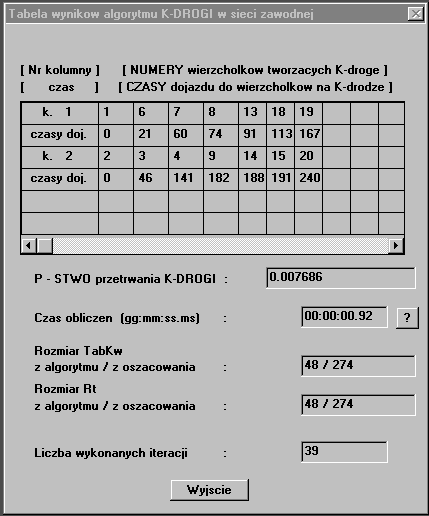
Rys. D.5 Okno dialogowe wyników działania algorytmu NRKD w sieci zawodnej

Wyniki symulacji (np. prawdopodobieństwo optymalności rozwiązania) wyświetlane są na bieżąco w trakcie symulacji, w postaci tzw. monitorów. Ponadto wyniki te zapisywane są w pliku tekstowym o rozszerzeniu "*.mcw". W module zawarto także opcje umożliwiające porównanie złożoności obliczeniowej badanych algorytmów poprzez porównanie czasów ich realizacji (porównaj z rys. D.5).

Rys. D.6 Okno dialogowe badania optymalności rozwiązania z algorytmu NRKD

Moduł czwarty umożliwia przeprowadzenie badań symulacyjnych algorytmów wyznaczających K-drogę najkrótszą w warunkach zawodnej struktury sieci.

W celu przeprowadzenia tych badań należy podać (rys. D.7):

- jeden z modeli sieci, dla której przeprowadzamy badania (model ten zawiera już plan niszczenia sieci) - opcja "Plik" z rys. D.1;
- liczbę K kolumn obiektów podlegających przegrupowaniu;
- K-wierzchołki: początkowy i^s i końcowy i^d;
- długości czasowe poszczególnych kolumn;
- liczbę E eksperymentów;
- górne ograniczenie na czas przegrupowania K kolumn;
- algorytm etapowy;
- rodzaj częstości (oraz ewentualnie parametr) otrzymywania informacji o stanie struktury sieci.

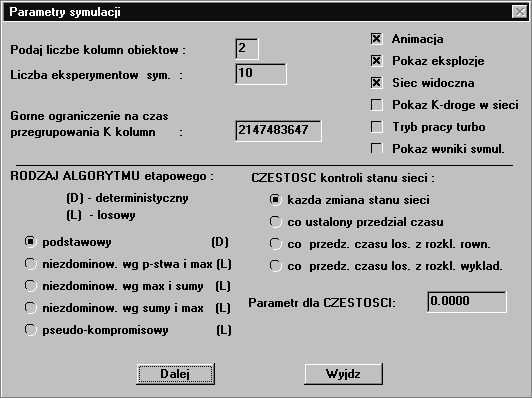
Rys. D.7 Okno dialogowe parametrów symulacyjnego badania algorytmów wyznaczania K-drogi w sieci zawodnej

Wyniki symulacji zostają przedstawione w postaci graficznej (np. wykres funkcji prawdopodobieństwa realizacji poszczególnych K-dróg) oraz w postaci tekstowej (np. czasy realizacji poszczególnych K-dróg). Ponadto wyniki te zostają zapisane w plikach zewnętrznych o rozszerzeniach "*.mdb" i "*.sym".

LITERATURA

[1]	Ameljańczyk A. :	Optymalizacja wielokryterialna, Wojskowa Akademia Techniczna, Warszawa 1986.
[2]	Ameljańczyk A. :	Teoria gier, Wojskowa Akademia Techniczna, Warszawa 1978.
[3]	Ahuja R.K., Magnanti T.L., Orlin J.B. :	Network Flows: Theory, Algorithms and Applications, Prentice Hall, Englewood Cliffs, 1993.
[4]	Aneja Y.P., Nair K.P.K.:	The constrained shortest path problem, Naval Res. Logistics Quart. 25 (1978), 549-556.
[6]	Banachowski L., Kreczmar A. :	Elementy analizy algorytmów, WNT, Warszawa 1982.
[7]	Banachowski L., Kreczmar A.,Rytter W :	Analiza algorytmów i struktur danych, WNT, Warszawa 1987.
[8]	Banachowski L., Diks K., Rytter W. :	Algorytmy i struktury danych, WNT, Warszawa 1996.
[9]	Barczak A. :	Komputerowe gry wojenne, Wyd. Bellona, Warszawa 1996.
[10]	Bloniarz P. :	A shortest path algorithm with expected time O(n²log n logn), Proc. 12th Ana. ACM Symp. on Theory of Computing*, Los Angeles 1980, 378-384.
[11]	Błażewicz J. :	Złożoność obliczeniowa problemów kombinatorycznych, WNT, Warszawa 1988.
[12]	Bobrowski D. :	Probabilistyka w zastosowaniach technicznych, WNT, Warszawa 1986.
[13]	Cai X., Kloks T., Wong C.K. :	Time-varying shortest path problems with constraints. Networks 29 (1997), 141-149.
[14]	Brandt S. :	Analiza danych, PWN, Warszawa 1998.
[15]	Chojnacki A. :	Modelowanie matematyczne, Wojskowa Akademia Techniczna, Warszawa 1986.
[16]	Chojnacki A., Piasecki S.:	Planowanie operacji wojennych, Wojskowa Akademia Techniczna, Warszawa 1973.
[17]	Chudy M.:	Elementy analizy algorytmów i obliczeń równoległych, Wojskowa Akademia Techniczna, Warszawa 1998.
[18]	Chudy M.:	Programowanie matematyczne, cz.II, Wojskowa Akademia Techniczna, Warszawa 1979.
[19]	Chudy M.:	Programowanie matematyczne, cz.I, Wojskowa Akademia Techniczna, Warszawa 1979.
[20]	Chudy M.:	Wybrane algorytmy transformacji obrazów binarnych i wielokolorowych zapisanych w postaci liniowego quadtree, Postępy Cybernetyki 1, 1992, 15-24.
[21]	Chudy M.:	Algorytm konstrukcji quadtree obrazu wynikowego, otrzymanego z obrazów pierwotnych, spełniający zadaną funkcję na kolorach tych obrazów, Postępy Cybernetyki 4, 1993, 53-60.
[22]	Cielątkowski J. :	Niektóre problemy sieci transportowych uwarunkowanych czasowo, Materiały IV Krajowej Konferencji Badań Operacyjnych i Systemowych, Gdynia 1995.
[23]	Corea G.A., Kulkarni V. G. :	Minimum cost routing on stochastic networks, Operations Research 38 (1990), 527-536.
[24]	Cormen T.H., Leiserson Ch.E., Rivest R.L. :	Wprowadzenie do algorytmów, WNT, Warszawa 1997.
[25]	Czujew J. :	Badania operacji w wojsku, Wydawnictwo MON, Warszawa 1972.
[26]	Daellenbach H.G., De Kluywer C.A. :	Note on multiple objective dynamic programming, Journ. Opnl. Research Society 31 (1980), 591-594.
[27]	Dantzig G.B. :	All shortest routes in a graph, w P. Rosentiehl (red.): Theory of Graphs, Gordon and Brench, New York 1967, 91-93.
[28]	Denardo E.V.,Fox B.L.:	Shortest-route methods: 1. Reaching, pruning and buckets, Operations Research 27 (1979), 215-248.
[29]	Deo N. :	Teoria grafów i jej zastosowanie w technice i informatyce, WNT, Warszawa 1980.
[30]	Deo N., Kowalik J., Sysło M. :	Algorytmy optymalizacji dyskretnej, wyd. II, PWN, Warszawa 1995.
[31]	Deo W., Pang Chi-yin :	Shortest path algorithms - Taxonomy and Annotation, Networks 14 (1984), 275-329.
[32]	Dial P.B., Glover F., Karney D., Klingman D.:	A computational analysis of alternative algorithms and labeling techniques for finding shortest path trees, Networks 9 (1979), 215-248.
[33]	Dijkstra E. :	A note on two problems in connection with graphs, Numerische Mathematik 1 (1959), 269-271.
[34]	Dresher M. :	Games and Strategy. Theory and Applications, Prentice-Hall, Englewood Cliffs 1961.
[35]	Dreyfus S. E. :	An appraisal of some shortest path algorithms, Operations Research 17 (1969), 395-412.
[36]	Dyson R. G. :	Maximin programming, fuzzy linear programming and multi-criteria decision making, Journal Operat. Res. Society 31 (1980), 263-267.
[37]	Feller W. :	Wstęp do rachunku prawdopodobieństwa.Tom II, PWN, Warszawa 1978.
[38]	Filar W. :	Badania operacyjne a problemy zaopatrywania i obsługi wojsk, Wydawnictwo MON, Warszawa 1973.
[39]	Findeisen W. (red.) :	Analiza systemowa - Podstawy i metodologia, PWN, Warszawa 1985.
[40]	Fisz M. :	Rachunek prawdopodobieństwa i statystyka matematyczna, PWN, Warszawa 1958.
[41]	Fishman G.S. :	Symulacja cyfrowa. Koncepcje i metody, PWE, Warszawa 1981.
[42]	Floyd R.W. :	Algorithm 97. Shortest Path, Commun. of the ACM 5 (1962), p.345.
[43]	Fox B. L. :	More on kth shortest paths, Comm. Assoc. Comput. Mach. 18 (1975), 279.
[44]	Frank H. :	Shortest paths in probabilistic graphs, Operations Reseach 17 (1969), 583-599.
[45]	Fredericksen G.N. :	Shortest path problem in planar graphs, 24th Ann. Symp. Found. Comput. Sci., Tucson, Ariz, 7-9 November 1983, N.Y.: Silver Spring, Md, 1983, 242-247.
[46]	Fredman M.L. :	New bounds on the complexity of the shortest path problem, SIAM Journ. Comp. 6 (1976), 83-89.
[47]	Gajek L., Kałuszka M.:	Wnioskowanie statystyczne. Modele i metody, WNT, Warszawa 1996.
[49]	Garey M., Johnson D. :	Computers and Intractability: A Guide to the Theory of NP Completeness, W. H. Freeman, San Francisco 1979.
[50]	Gaździcki J. :	Informatyka w geodezji i kartografii, Państw. Przeds. Wydawn. Kartogr., Warszawa 1975.
[51]	Gaździcki J. :	Systemy informacji przestrzennej. Państw. Przeds. Wydawn. Kartogr., Warszawa 1990.
[52]	Golden B. :	Shortest path algorithms: a comparisons, Operations Research 24 (1976), 1164-1168.
[53]	Golden B.L., Skiscim C.C.:	Solving k-shortest and constrained shortest path problems efficiently, Network Optimization and Applications 20 (1989), Texas A&M University, College Station.
[54]	Grace M. J.,Potts R.B. :	The diffusion of traffic platoons, Operations Research, 12 (1964), 255-274.
[55]	Gruźlewski T.,Weiss Z.:	Programowanie współbieżne i rozproszone w przykładach i zadaniach, WNT, Warszawa 1993.
[56]	Gutenbaum J. :	Modelowanie matematyczne systemów, Omnitech Press, Warszawa 1992.
[57]	Hamacher H.W., Queyranne M. :	K best solutions to combinatorial optimization problems, Annals of Operations Research 4 (1985/6), pp.123-143.
[58]	Handler G.Y., Zang I.:	A dual algorithm for the constrained shortest path problem, Networks 10 (1983), 293-310.
[59]	Hassan M.M.D. :	Network reduction for the acyclic constrained shortest path problem, Eur. Journ. Oper. Res. 63 (1992), 121-132.
[60]	Hoffman W.,Pavley R. :	A method for the solution of the Nth best path problem, Assoc. Comput. Mach. 6 (1959), 506-514.
[61]	Howard R. :	Programowanie dynamiczne i procesy Markowa, Wydawnictwo MON, Warszawa 1970.
[62]	Ibaraki T., Katon N., Mine H. :	An O(Kn²) algorithm for K shortest simple paths in an undirected graph with nonnegative arc length, Trans. Inst. Electron. and Comm. Eng. Jap. 12 (1978), 1199-1206.
[63]	Iositescu M. :	Skończone procesy Markowa i ich zastosowania, PWN, Warszawa 1988.
[64]	Jankowski M. :	Elementy grafiki komputerowej, WNT, Warszawa 1990.
[65]	Johnson D. B. :	Efficient algorithms for shortest paths in sparse networks, Journal Assoc. Comp. Mach. 24 (1977), 1-13.
[66]	Kaliszewski I., Słomiński L.:	Problemy równoległej optymalizacji dyskretnej, IBS PAN, Warszawa 1994.
[67]	Karlsson P.G., Poblete P.V. :	An O(m log log D) algorithm for shortest path, Discrete Appl. Math. 6 (1983), 91-93.
[68]	Karpiński J.,Korczak E:	Metody oceny niezawodności dwustanowych systemów technicznych, Omnitech Press, Warszawa 1990.
[69]	Kaszubowski Z., Mizera R., Piasecki S. :	Problemy przegrupowania wojsk, Wojskowa Akademia Techniczna, Warszawa 1970.
[70]	Kaufmann A., Faure R:	Badania operacyjne na co dzień, PWN, Warszawa 1968.
[71]	Kofler E. :	Podejmowanie decyzji przy niepełnej informacji, Real Publishers, Warszawa 1993.
[72]	Korzan B. :	Elementy teorii grafów i sieci, Metody i zastosowania. WNT, Warszawa 1978.
[73]	Korzan B. :	Grafy, hipergrafy i sieci, Wojskowa Akademia Techniczna, Warszawa 1980.
[74]	Korzan B. :	Metoda wyznaczania dróg kompromisowych w zawodnych sieciach skierowanych, Biuletyn WAT, Rok XXXI, Nr 7 (1982), 21-36.
[75]	Korzan B. :	Metoda wyznaczania dróg niezdominowanych w zawodnych sieciach skierowanych, Biuletyn WAT, Rok XXXII, Nr 11 (1983), 21-33.
[76]	Korzan B. :	Optymalizacja dróg w zawodnych sieciach skierowanych, Biuletyn WAT, Rok XXXII, Nr 6 (1983), 69-85.
[77]	Korzan B. :	Teoria grafów i sieci. Drogi ekstremalne w sieciach skierowanych, Wojskowa Akademia Techniczna, Warszawa 1977.
[78]	Korzan B. :	Teoria niezawodności, Wojskowa Akademia Techniczna, Warszawa 1983.
[79]	Koziej S., Łaski W., Sznajder R. :	Teren i taktyka, Wydawnictwo MON, Warszawa 1980.
[80]	Krysicki W., Bartos J., Dyczka W., Królikowska K., Wasilewski M. :	Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach - cz.II. Statystyka matematyczna, WNT, Warszawa 1994.
[81]	Kucharczyk J., Sysło M.:	Algorytmy optymalizacji w języku ALGOL 60, PWN, Warszawa 1977.
[82]	Kukuła K. (red.):	Badania operacyjne w przykładach i zadaniach, PWN, Warszawa 1996.
[83]	Kulikowski J. L. :	Zarys teorii grafów, PWN, Warszawa 1986.
[84]	Kulikowski R., Sosnowski J.S. :	Badania systemowe, cz.II - Metody optymalizacji i sterowania komputerowego, Omnitech Press, Warszawa 1990.
[85]	Kulkarni V.G., Adlakha V.G. :	Markov and Markov-regenerative PERT networks, Operations Research 34 (1986), pp. 769-781.
[86]	Lawler E. L. :	Comment on computing the k shortest paths in graph, Comm. Assoc. Comp. Mach. 20 (1977), 603-604.
[87]	Lawler E.L. :	A procedure for computing the K best solutions to discrete optimization problems and its applications to the shortest path problem, Management Science 18 (1972), pp. 401-407.
[88]	Lev G.F., Pippenger N., Valiant L.G. :	A fast parallel algorithm for routing in permutation networks, IEEE Trans. on Computers C-30 (1981), 93-100.
[89]	Libura M. :	Wykorzystanie podzbiorów rozwiązań najlepszych do oceny dokładności rozwiązań zadań optymalizacji dyskretnej z zaburzeniami funkcji celu, Materiały IV Krajowej Konferencji Badań Operacyjnych i Systemowych BOS95, Gdynia 1995, str. 150-157.
[90]	Lofgren C. B. :	Reconstructing shortest paths, Network Optimization and Applications 20 (1989), Texas A&M University, College Station.
[91]	Loui R. P. :	Optimal paths in graphs with stochastic or multidimensional weights, Comm. Assoc. Comp. Mach. 26 (1983), 670-676.
[92]	Luce R.D., Raiffa H. :	Gry i decyzje, PWN, Warszawa 1964.
[93]	Łaski W.,Stasiewicz H :	Topografia wojskowa, Wydawnictwo MON, Warszawa 1983.
[95]	Minieka E. :	On computing sets of shortest path in a graph, Comm. Assoc. Comput. Mach. 17 (1974), 351-353.
[96]	Mirchandani P. :	Shortest distance and reliability of probabilistic networks, Comp. Oper. Res. 3 (1976), 347-355.
[97]	Mitchell G.H. :	Operational Research: Techniques and examples, The English Universities Press Ltd., National Coal Board 1972.
[98]	Mizera R. :	Algorytmy planowania transportu, Wojskowa Akademia Techniczna, Warszawa 1972.
[99]	Mizera R. :	Optymalizacja planowania przegrupowania wielu kolumn, Biuletyn WAT, Rok XIX, Nr 4 (1970), 47-58.
[100]	Morse P. M., Kimball G. E.:	Methods of Operations Research, The Technology Press of Massachusetts Institute of Technology & John Wiley & Sons, Inc. New York 1953.
[101]	Murthy J., Olson D.L., Shetty B., Venkataramanau M.A. :	Network reoptimization procedures for multiobjective network problems, Network Optimization and Applications 20 (1989), Texas A&M University, College Station.
[102]	Nowak M. :	Właściwości taktyczne terenu, Akademia Sztabu Generalnego, Warszawa 1974.
[103]	Nowicki T. :	Modelowanie matematyczne. Metody symulacyjne, Wojskowa Akademia Techniczna, Warszawa 1994.
[104]	Owen G. :	Teoria gier, PWN, Warszawa 1975.
[105]	Papadimitriou Ch.H.:	Combinatorial Optimization: Algorithms and Complexity, Prentice-Hall, Englewood Cliffs 1989.
[106]	Piasecki S. :	Optymalizacja marszruty na istniejącej sieci dróg, Biuletyn WAT, Rok XV, Nr 9 (1966), 65-82.
[107]	Piasecki S. :	Elementy teorii niezawodności i eksploatacji urządzeń, Wojskowa Akademia Techniczna, Warszawa 1974.
[109]	Pierce A.G. :	Bibliography on algorithms for shortest path, shortest spanning tree and related circuit routing problems (1956-1974), Networks 5 (1975), 129-149.
[110]	Pollack M. :	The kth best route through a network, Operations Research 9 (1961), 578-580.
[111]	Pritsker A.B., Sigal E.C., Solberg J.J.:	The stochastic shortest route problem, Operations Research 28 (1980), 1122-1129.
[112]	Reingold E.M., Nievergelt J., Deo N. :	Algorytmy kombinatoryczne, PWN, Warszawa 1985.
[113]	Ross K., Wright Ch.:	Matematyka dyskretna, PWN, Warszawa 1996.
[114]	Ruciński A., Palka Z. :	Niekonstruktywne metody matematyki dyskretnej, WNT, Warszawa 1996.
[115]	Sahni S.K. :	Algorithm for scheduling independent tasks, Journal of the ACM 23 (1976), pp. 116-127.
[116]	Shier D.R :	Iterative methods for determining the K shortest path in a network, Networks 6 (1976), 205-229.
[117]	Sienkiewicz P. :	Inżynieria systemów. Wybrane zastosowania wojskowe, Wydawnictwo MON, Warszawa 1983.
[119]	Skibiński J., Filar W., Bijak E., Szpilberg I. :	Zastosowanie metod badań operacyjnych do rozwiązywania niektórych zagadnień wojskowych, Akademia Sztabu Generalnego, Warszawa 1964.
[120]	Spira P.M. :	A new algorithm for finding all shortest paths in a graph of positive arcs in average time O(n² log²n). SIAM Jour. Comput. 2 (1973), 28-32.
[121]	Stearns S.D. :	A mathematical model for strategic movement, Operations Research 12 (1964), 237-254.
[122]	Stępak J. :	Ocena wpływu elementów fizycznej dostępności lądowego teatru działań wojennych na efektywność walki zbrojnej, Rozprawa habilitacyjna, Akademia Sztabu Generalnego, Warszawa 1990.
[123]	Sznajder R.J. :	Taktyczna ocena terenu w działaniach bojowych pułku, Akademia Sztabu Generalnego, Warszawa 1984.
[124]	Tarapata Z. :	Algorithm for simultaneously finding a few independent shortest paths, Conference Proceedings from 9th European Simulation Symposium, pp. 89-93, Passau 1997.
[125]	Tarapata Z. :	The method of evaluation the characteristics of conflict situation modelled by operational game, Biuletyn WAT, Rok XLVII, 3 (1998), 21-40.
[126]	Tarapata Z. :	Symulacja przemieszczania środków walki- -pojedynczych, grupowych i oddziałów, w Opracowaniu wewnętrznym WAT z grantu nr 0S001 015 07, Wojskowa Akademia Techniczna, Warszawa 1996.
[127]	Tarapata Z. :	Algorytmy przemieszczania wojsk w warunkach oddziaływania przeciwnika, w Opracowaniu wewnętrznym WAT z grantu nr T00A 011 10, Wojskowa Akademia Techniczna, Warszawa 1997.
[128]	Tarapata Z. :	Wyznaczanie optymalnego planu równoczesnego przegrupowania (manewru w sensie przemarszu) wielu kolumn, w Opracowaniu wewnętrznym WAT z grantu nr T00A 011 10, Wojskowa Akademia Techniczna, Warszawa 1996.
[129]	Tarapata Z. :	Metoda przygotowania i obróbki statystycznej danych eksperymentu symulacyjnego dla wybranej klasy systemów, Praca magisterska, Wojskowa Akademia Techniczna, Warszawa 1995.
[131]	Tomaszewski A.:	Założenia i koncepcja komputerowej gry wojennej pk.Model-Gra. cz.III. Koncepcja komputerowego odwzorowania manewru w operacji i walce, Akademia Obrony Narodowej, Warszawa 1995.
[132]	Tyszer J. :	Symulacja cyfrowa. WNT, Warszawa 1990.
[133]	Ulicki M. :	Metoda modelowania dynamiki obiektów dla potrzeb informatycznego wspomagania dowodzenia, Rozprawa doktorska, Wojskowa Akademia Techniczna, Warszawa 1997.
[134]	Van Slyke R. :	Stochastic aspects of networks. Networks 5 (1975), 97-100.
[135]	Van Vliet D. :	Improved shortest path algorithm for transportation networks, Transport. Res. 12 (1978), 7-20.
[136]	Wagner R. A. :	A shortest path algorithm for edge-sparse graphs, Journal Assoc. Comp. Mach. 23 (1976), 50-57.
[137]	Warburton A. :	Approximation of Pareto optima in multiple-objective, shortest-path problems, Operations Research 35 (1987), 70-79.
[138]	Welch P. :	The statistical analysis of simulation results, Academic Press, New York 1983.
[139]	Wendell R. :	Multiple objective mathematical programming with respect to multiple decision-makers, Operation Research 28 (1980), pp.1100-1111.
[140]	White D.J. :	The set of efficient solutions for multiple objective shortest path problems, Comp. Oper. Res. 9 (1982), 101-107.
[141]	White D.J. :	Optimality and Efficiency, John Wiley & Sons, New York, 1982.
[143]	Wirth N. :	Algorytmy + struktury danych = programy, WNT, Warszawa 1989.